Какой максимальный вращающий момент и как его можно увеличить?

Максимальный крутящий момент

Максимальным называется крутящий момент, представляющий пик, после которого момент не растет, несмотря на количество оборотов. На малых оборотах в цилиндре скапливается большой объем остаточных газов, в результате чего показатель КМ значительно ниже пикового. На средних оборотах в цилиндры поступает больше воздуха, процент газов снижается, крутящий момент продолжает расти.

При высоких оборотах растут потери эффективности: от трения поршней, инерционных потерь в ГРМ, разогрева масла и т.д. будет зависеть работа мотора. Поэтому рост качества работы двигателя прекращается или само качество начинает снижаться. Максимальный крутящий момент достигнут и начинает снижаться.

Отзывы

Общие сведения

Момент инерции — это свойство тела противостоять изменению скорости вращения. Чем момент инерции выше — тем больше это противостояние. Момент инерции часто сравнивают с понятием массы для прямолинейного движения, так как масса определяет, насколько тело сопротивляется такому движению. Распределение массы по объему тела не влияет на прямолинейное движение, но имеет большое значение при вращении, так как от него зависит момент инерции.

В центробежном регуляторе скорость вращения двигателя контролируется с помощью момента инерции: с достижением определенной скорости количество топлива, подаваемого в двигатель, уменьшается. Двигатель вращает два шара в верней части устройства, и, при увеличении скорости они расходятся, увеличивая момент инерции всего устройства. Когда момент инерции достигает определенной величины, это устройство ограничивает поступление топлива.

Определить момент инерции для тел простой геометрической формы и с постоянной плотностью можно, используя общепринятые формулы. Для тел более сложных форм используют математический анализ. В зависимости от того, как вес распределен внутри тел, два тела с одинаковой массой могут иметь разный момент инерции. Например, момент инерции I для однородного шара, с одинаковой по всему объему плотностью, находят по формуле:

Тут m — это масса шара, а r — его радиус. Если взять два шара одинаковой массы, с радиусом первого вдвое больше радиуса второго, то момент инерции большего шара будет в 2²=4 раза больше первого. В этой формуле радиус — это расстояние от центра вращения до наиболее удаленной от этого центра точки на теле, для которого измеряется момент инерции. Если взять цилиндр с массой m, которая равна массе одного из шаров выше, и с расстоянием L от центра вращения до самой удаленной точки, так что эта величина равна радиусу этого шара, то момент инерции цилиндра I будет равен:

в случае, если цилиндр вращается вокруг его основания. Момент инерции будет равен:

если цилиндр вращается вокруг оси, проходящей через его центр по длине. При таком вращении цилиндр становится похожим на пропеллер. Вторую формулу легко получить из первой: радиус от центра вращения до наиболее удаленной точки равен половине длины цилиндра, но так как этот радиус возведен в квадрат, то 1/2 L (или r) становится 1/4 L² (или r²). В любом случае, глядя на эти формулы, легко заметить, что форма тела и даже просто смещение центра вращения существенно влияют на момент инерции. Момент инерции играет важную роль в спорте и в механике, и его регулируют, изменяя массу или форму предметов и даже тела спортсмена.

Потребляемая мощность электродвигателя

Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.

В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).

Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.

И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.

Число пусков электродвигателя в час

Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.

Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.

Способы прироста в крутящем моменте двигателя

Величину, которая необходима для крутящего момента той или иной модели автомобиля, определяют инженеры ещё на предварительном этапе конструкторской разработки мотора. От неё зависят и другие элементы автомобиля: его подвеска, тормозное и рулевое управление, аэродинамика

Поэтому, прежде чем приступать к самостоятельному форсированию двигателя, важно убедиться, что машина не развалится от умощнения двигателя

Способов увеличения крутящего момента и, вместе с ним, мощности двигателя, может быть много:

• изменение геометрических свойств поршневой группы;
• увеличение компрессии;
• замена инжекторов или форсунок;
• установка наддува на атмосферный двигатель;
• изменения в системе воздухозабора;
• доработка или замена системы выпуска выхлопных газов;
• чип-тюнинг, при помощи перепрограммирования топливной карты блока управления мотора.

Однако принудительное увеличение крутящего момента и мощности двигателя в значительной степени уменьшает ресурс его работы.

Абсолютная величина момента силы

Определение

Абсолютной величиной момента силы признается величина, равная произведению абсолютного значения на плечо данной силы относительно выбранной точки.

Рассмотрим рисунок, приведенный ниже.

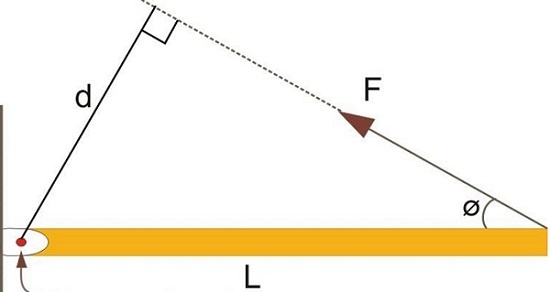
Здесь продемонстрирован стержень с длиной L. Так, с одной стороны он закрепляется шарнирным соединением к вертикальной плоскости, другой его конец — свободен. На него воздействует F¯. Угол между стержнем и вектором равняется φ. Вращающийся момент следует определить через векторное произведение. Его модуль равняется произведению: абсолютные значения, умноженные на синус угла между ними.

Используя формулы из тригонометрии, прибегаем к следующему равенству:

\(M\;=\;L\ast F\ast\sin(\varphi)\)

Возвращаясь к рисунку, переписываем равенство в форму:

\(M\;=\;d\ast F\)

Здесь \(d = L*sin(φ)\) — это величина, равная расстоянию от вектора силы оси вращения. F образует больший момент при большем d.

Момент силы

В динамике вращательного движения важна не непосредственно величина силы, а произведение этой величины на расстояние от точки вращения. Это произведение называется моментом силы, обозначается буквой $M$:

$$M=F_\tau R$$

Из приведенной формулы можно получить размерность момента: поскольку сила измеряется в ньютонах, а радиус — в метрах, единица измерения момента силы получается равной ньютон-метру. Радиус вращения при этом нередко называют «плечом силы» $l$.

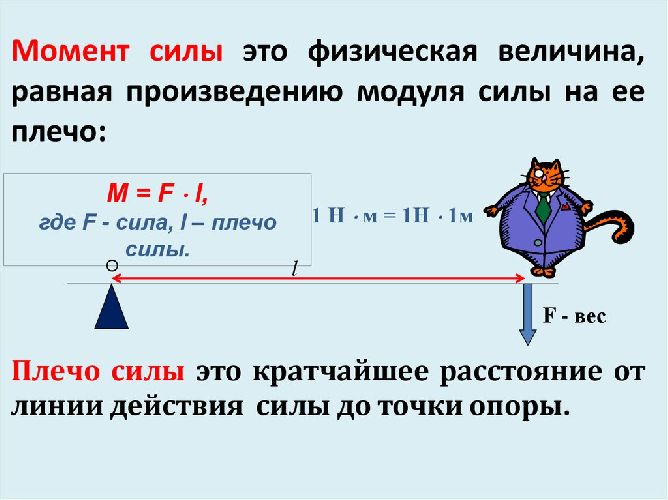
Рис. 2. Момент силы.

Обратите внимание, что вращательное движение создает только компонента силы, направленная перпендикулярно радиусу поворота, — тангенциальная составляющая силы:

$$F_\tau = F sin \alpha,$$

где $\alpha$ — это угол между радиус-вектором точки, к которой приложена сила $F$, и вектором приложения этой силы.

В самом деле, если сила направлена от точки приложения точно в сторону оси вращения, никакого вращательного движения создать с помощью этой силы не получится, какой бы модуль у этой силы не был. Формула также подтверждает это — синус угла между вектором силы, направленной точно на ось, и радиус-вектором точки приложения равен нулю, а значит, и тангенциальная составляющая силы также будет равна нулю. Момент такой силы, соответственно, также будет нулевым. Создать вращение будет невозможно.

Вращение невозможно создать также в случае, когда сила приложена непосредственно к оси вращения, независимо от ее направления. Радиус-вектор точки приложения силы при этом равен нулю, и определить тангенциальную составляющую приложенной силы невозможно. Момент такой силы оказывается нулевым.

Единицы

Момент силы имеет размерность «сила на расстояние» и единицу измерения ньютон-метр в системе СИ. Энергия и механическая работа также имеют размерность «сила на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина (псевдо) векторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, приложенный через целый оборот, совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоулей. Математически:

E=Mθ,{\displaystyle E=M\theta ,}

где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.

Аквапарки

Геленджик, достопримечательности и развлечения которого подойдут для разных возрастных категорий, располагается в окружение гор и моря.

В самом городе и в его окрестностях можно побывать в нескольких аквапарках:

1. Аквапарк «Дельфин» (ул. Революционная, 8).

Аквапарк работает в летний период без выходных с 9 утра до 10 вечера.

• для детей вход стоит 300 руб.;
• для взрослых – 500 руб.

На Центральном пляже под открытым небом находится аквапарк «Дельфин». Посетителям предлагаются спуски на нескольких видах горок. Имеются прекрасные бассейны.

2. Аквапарк «Золотая бухта» (ул. Туристическая, 23).

Пейзаж аквапарка «Золотая бухта», курорт Геленджик

Летом с 9 до 7 можно посетить аквапарк «Золотая бухта».

• дети, рост которых не превышает 1 м 5 см, проходят бесплатно;
• взрослые и дети свыше 145 см оплачивают билет на день – 1700 руб.;
• дети от 106 до 144 см – 900 руб.

Водные аттракционы занимают площадь в 15 га. Здесь имеется почти 60 горок и 8 бассейнов для всех возрастов. Отдыхающие могут позагорать на шезлонгах или поиграть на спортивных площадках.

3. Аквапарк «Бегемот» (ул. Луначарского, 159).

Аквапарк работает с мая по сентябрь с 10 до 7.

Стоимость посещения:

• взрослые на целый день – 1300 руб.;
• взрослые на вторую половину дня 1200 руб.;
• дети до 140 см на весь день – 750 руб., с 2 до 7 – 650 руб.;
• дети с ростом до 1 м – вход свободный.

На 1,5 га расположилось 15 горок и 3 бассейна разной глубины. Предусмотрены места для отдыха под зонтиками и несколько кафе.

Примеры момента силы

Здесь момент силы каждого ребенка равен весу этого ребенка, умноженному на его расстояние от оси вращения. Девочка сидит ближе к точке опоры, но прилагает больше силы к качелям, чем мальчик, поэтому качели — в равновесии.

Хороший пример момента силы в быту — это действие на тело одновременно момента силы и изгибающего момента, о котором мы говорили выше. Момент силы часто используют в строительстве и в проектировании строительных конструкций, так как, зная момент силы, можно определить нагрузку, которую должна выдержать эта конструкция. Нагрузка включает нагрузку от собственного веса, нагрузку, вызванную внешними воздействиями (ветром, снегом, дождем, и так далее), нагрузку от мебели и нагрузку, вызванную посетителями и обитателями здания (их вес). Нагрузка, вызванная людьми и интерьером, называется в строительстве полезной нагрузкой, а нагрузка, вызванная весом самого здания и окружающей средой называется статической или постоянной нагрузкой.

При постройке в 1900 году моста Александры через реку Оттава использовано много двутавровых балок

Если на балку или другой конструктивный элемент действует сила, то в ответ на эту силу возникает изгибающий момент, под действием которого некоторые части этой балки сжимаются, в то время как другие, наоборот, растягиваются. Представим, к примеру, балку, на которую действует сила, направленная вниз и приложенная по центру. Под воздействием этой силы балка принимает вогнутую форму. Верхняя часть балки, на которую действует сила, сжимается под воздействием этой силы, в то время как нижняя, наоборот, растягивается. Если нагрузка больше, чем этот материал может выдержать, то балка разрушается.

Наибольшая нагрузка — на самый верхний и самый нижний слои балки, поэтому в строительстве и при проектировании сооружений эти слои часто укрепляют. Хороший пример — использование двутавровых конструкций. Двутавр — конструктивный элемент с поперечным сечением в форме буквы Н или латинской буквы “I” с верхней и нижней засечками (поэтому английском языке используют термин I-beam, Такая форма очень экономична, так как она позволяет упрочнить самые слабые части балки, используя при этом наименьшее количество материала. Чаще всего двутавровые балки сделаны из стали, но для прочной балки двутавровой конструкции вполне можно использовать и другие материалы. На YouTube можно найти видеосюжеты испытания двутавровых балок, сделанных из материалов, менее прочных, чем сталь, например из пенопласта и фанеры (нужно искать plywood beam test). Двутавровые балки из фанеры и древесностружечных плит появились на российском рынке стройматериалов относительно недавно, хотя они давно и очень широко применяются при строительстве каркасных домов в Северной Америке.

Если на конструкцию действует изгибающий момент, то двутавровые балки — решение проблем, связанных с прочностью. Двутавровые балки также используют в конструкциях, которые подвергаются напряжению сдвига. Края двутавровой балки противодействуют изгибающему моменту, в то время как центральная опора противостоит напряжению сдвига. Несмотря на ее достоинства, двутавровая балка не может противостоять крутящим нагрузкам. Чтобы уменьшить эту нагрузку на поверхность конструкции, ее делают круглой и полируют поверхность, чтобы предотвратить скопление нагрузки в точках с неровной поверхностью. Увеличение диаметра и изготовление такой конструкции полой внутри может помочь уменьшить ее вес.

Турбовинтовые двигатели с воздушными винтами создают крутящий момент, который действует на фюзеляж этого турбовинтового самолета; по-английски в данном случае могут говорить о моменте силы (moment of force) или о возникновении напряжения при кручении (torsional stress), так как вращение отсутствует

Специальные случаи

Формула момента рычага

Момент, действующий на рычаг

Очень интересен особый случай, представляемый как определение момента силы в поле:

|M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}

где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.

Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:

|T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}

Сила под углом

Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsin⁡θ{\displaystyle M=rF\sin \theta }.

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=,ΣV={\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM={\displaystyle \Sigma M=0}.

Момент силы как функция от времени

Момент силы — производная по времени от момента импульса,

Видеоурок: вращающий момент

M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}

где L→{\displaystyle {\vec {L}}} — момент импульса.

Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.

Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.

Lo→=Icω→+M(ro→−rc→),vc→.{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+.}

Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.

Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то

M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}

где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.

Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:

Mc→=Icdω→dt+w→,Icw→.{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+.}

Что такое крутящий момент

Крутящим моментом называют единицу силы, которая необходима для поворота коленчатого вала ДВС. Эта не «лошадиная сила», которой должна обозначаться мощность.

ДВС вырабатывает кинетическую энергию, вращая таким образом коленвал. Показатель мощности двигателя (сила давления) зависит от скорости сгорания топлива. Крутящий момент – результат от действия силы на рычаг. Эта сила в физике считается в ньютонах. Длина плеча коленвала считается в метрах. Поэтому обозначение крутящего момента – ньютон-метр.

Технически, крутящий момент – это усилие, которое должно осуществляться двигателем для разгона и движения машины. При этом сила, оказывающая действие на поршень, пропорциональна объему двигателя.

Маховик – одна из важнейших деталей, которая должна через редуктор передавать вращательный момент от мотора к коробке передач, от стартера на коленвал, от коленвала на нажимной диск. Собственно, крутящий момент – итог давления на шатун.

Крутящий момент у бензиновых и дизельных моторов

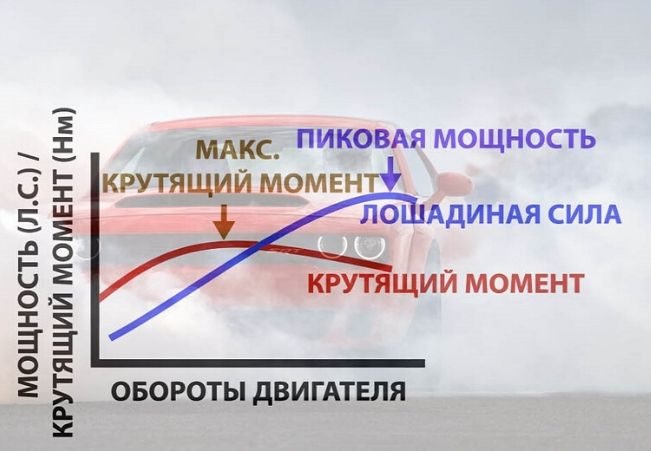
Бензиновые двигатели отличаются не самым большим крутящим моментом. Своего наибольшего значения крутящий момент бензинового двигателя достигает на оборотах не менее чем 3-4 тыс. об/мин. Однако бензиновый двигатель быстро сможет увеличить мощность и раскрутиться до 7-8 тыс. об/мин. При таких сверхвысоких оборотах мощность возрастает в разы.

Дизельный двигатель не отличается высокими оборотами. Обычно это 3-5 тыс. об/мин максимум, и тут он бензиновым моторам проигрывает. Однако крутящий момент дизельного двигателя выше в разы, и доступным он становится очень быстро, практически с холостого хода.

В качестве конкретного примера, можно вспомнить тесты двух двигателей от фирмы Ауди – один дизельный: 2.0 TDI мощностью 140 л.с. и крутящим моментом 320 Н.м, а второй бензиновый: 2.0 FSI мощностью 150 л.с. и крутящим моментом 200 Н.м. По итогам контрольной прогонки в различных режимах получается, что дизель на целых 30-40 л.с. мощнее бензинового двигателя в диапазоне от 1 до 4,5 тыс. оборотов. Поэтому и не сто́ит смотреть только на лошадиные силы. Бывает, что мотор с меньшим рабочим объёмом, но с высоким крутящим моментом показывает себя намного динамичнее, чем двигатель с большим рабочим объёмом, но низким крутящим моментом.

В технических характеристиках, которые указываются для каждого автомобиля и его двигателя, показатель максимального крутящего момента всегда указывается в сочетании с величиной оборотов, при которых такой крутящий момент может быть достигнут. При этом обычно считается: если максимальный крутящий момент может быть достигнут на оборотах до 4,5 тыс. об/мин., то такой двигатель можно назвать низкооборотным; а если более 4,5 тыс. об/мин – то высокооборотным.

При малом количестве оборотов в область сгорания поступает незначительное количество воздушно-топливной смеси за единицу времени, поэтому крутящий момент и мощность невелики. Увеличивая обороты, количество топливно-воздушной смеси (а вслед за ним и мощность, и крутящий момент) возрастают. Достигая значительных параметров, мощность начинает снижаться из-за механических потерь на трение механизмов; инерционных потерь; от недостаточного нагнетания воздуха (именуемого кислородным голоданием).

Из соображений обеспечения максимальных количеств поступающего воздуха в камеру сгорания даже на незначительных оборотах двигателя применяются системы турбированного наддува с электронным регулированием. Применяя такие системы турбонаддува, можно обеспечивать равномерность характеристик крутящего момента в широком диапазоне оборотов двигателя.

От чего зависит крутящий момент ДВС

Чтобы легче разобраться в этом
вопросе, посмотрим на график внешней скоростной характеристики (ВСХ) одного из
двигателей Jeep Grand Cherokee.

График ВСХ двигателя Jeep
График ВСХ двигателя Jeep Grand Cherokee

На картинке видно, что величина
момента меняется при увеличении скорости оборотов ДВС. После частоты 3500 об/мин
показатель резко падает. Почему так происходит? Суть в наполнении цилиндров
горючей смесью. Объем новой смеси не всегда равен объему камеры сгорания.
Данная характеристика называется коэффициентом
наполнения цилиндров. Величина может быть выше или ниже 1.

Изменение
коэффициента происходит ввиду строения впускного коллектора и настройки фаз газораспределения.
В нашем примере впускные клапаны ДВС открываются на 10° до верхней мертвой точки
и закрываются на 60° после прохождения нижней мертвой точки. Это сделано, чтобы
сбалансировать «полку» момента и получить оптимальные значения для средних
оборотов (частота вращения 2500-3500 в минуту), которые нам и нужны для
повседневной эксплуатации.

Что происходит с нашим
мотором, когда он работает на малых оборотах? В теории при уменьшении скорости
поршня должна улучшится наполняемость цилиндра. На практике при частоте вращения
1600 об/мин значение тягового усилия падает до 260 Ньютон-метров. Причина тому –
слишком позднее закрытие клапана и малая степень сжатия (7.4/1 вместо 9/1). Как
итог – меньшее давление газов в конце такта сгорания, и соответственно, малый
крутящий момент двигателя.

И напоследок

Способ подогрева жиклеров омывателя без использования электричества

Расчет по массе и времени разгона от нуля до сотни

Определить как измеряется мощность двигателя, можно также по общей массе авто и времени его разгона до 100 километров в час. К сожалению, у этого способа есть один крупный недостаток — итоговая формула является достаточно сложной и она может сильно меняться в зависимости от технических особенностей авто (тип привода, характер трансмиссии и так далее).

Поэтому мы Вам рекомендуем производить расчет мощности по массе и времени разгона не вручную, а с помощью готового калькулятора на нашем сайте.

Оптимальный алгоритм действий:

1. Выполните разгон своего автомобиля от 0 до 100 километров в час. Определите время разгона любым удобным способом (обычно это делается с помощью бортового компьютера).
2. Узнайте массу своей машины — сделать это можно с помощью все того же бортового компьютера, с помощью технической документации и так далее.
3. Воспользуйтесь нашим калькулятором — введите массу и время разгона, выберите тип привода, укажите трансмиссию.

Предыстория

Файл:Moment Sili2.JPG

Момент силы

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .